Graph Coloring with Applications

Prepared by:

Joseph Malkevitch
Department of Mathematics
York College (CUNY)
Jamaica, New York 11451

email:

malkevitch@york.cuny.edu

web page:

http://york.cuny.edu/~malk


This article originally appeared as a web based Feature Column of the American Mathematical Society in 2003.


1. Introduction

The four-color problem, dating from 1852, was posed in the language of coloring the regions of a map. However, one can not seriously claim that it was applications that motivated this problem. Almost from the beginning the four-color problem thrived as a question in theoretical mathematics and the ideas and methods that were marshalled in attempts to solve the problem showed little explicit concern for applicability.

However, as has usually been the case with mathematics, as the theory of coloring the edges, vertices, and faces matured, it became clear that there were applicable problems which were illuminated by the work being done to get insight into coloring problems.

2. Resolving conflicts (I)

Imagine that a state legislature has 9 committees that must meet every Thursday. Ideally, the committees meet in any one of two special legislative hearing rooms where there are special microphones and other equipment to facilitate the recording of the committees' business, and where there are seats for the public when the hearings are open to the public. Sometimes scheduling a meeting in a room other than a special hearing room is also a possibility. Some of these committees have members in common, that is, there are people who serve on several different committees. Since people can not be in two places at one time, it would be very desirable to have committees with common members meet at different times. The committee names are a, b, ..., h and the table below indicates with an X when a pair of committees has one or more people on both committees.

	a	b	c	d	e	f	g	h
a			X	X	X	X	X
b						X	X
c	X					X
d	X				X	X	X	X
e	X			X
f	X	X	X	X			X
g	X	X		X		X		X
h				X			X

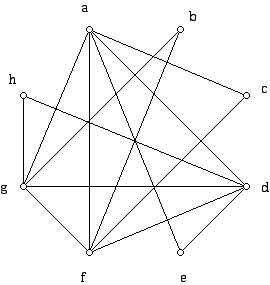
For example, since there is no X in the c row and e column (or the e row and c column), these two committees have no member in common. On the other hand, committees a and d have a least one member in common. Our first goal is to try to schedule these committees in as few time slots as possible. Furthermore, if there is a solution that uses as few time slots as possible which requires the use of two or fewer special rooms at a given time, that would be ideal. To construct a mathematical model of this situation, we represent each committee by a dot (vertex) and join two committees by a line segment (edge) if the vertices that represent them correspond to committees that have an X in the cell corresponding to these committees in the table above. The result is the graph below:

Since two vertices in this graph are joined together with an edge if and only if the committees must meet at different times, the minimum number of time slots to schedule the committees in can be found by computing the (vertex) chromatic number of this graph! Obviously, it is possible to color the vertices of the graph above with 8 colors because one can color each vertex with a different color. This is not the best answer. The coloring below uses 5 colors.

Figure 1

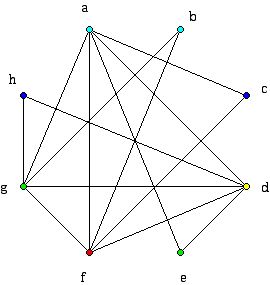
You can try to find the chromatic number of the graph above by trial and error or using one of the many graph-coloring algorithms that have been investigated to see if you can do better than 5 colors. But the theoretical news is not good. The problem of finding the vertex chromatic number for a graph is known to be an NP-complete problem. This means that it is not likely that a "fast" (e.g. polynomial time in the number of vertices) algorithm will ever be found which computes the smallest number of colors needed to color the vertices of a given graph. However, since this graph is not very large, finding its chromatic number is not difficult. In this case redrawing the graph above gives an insight:

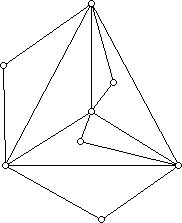
This isomorphic drawing (i.e. drawing with the same structure) of the graph in Figure 1 is a plane graph and, thus, by the four-color theorem its vertices can be colored with 4 or fewer colors. You should find a 4-coloring for yourself and label the vertices in a way which shows that it has the same structure as the original graph.

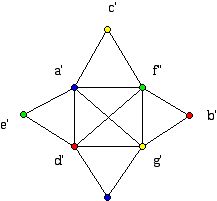
Below is shown yet another drawing of Figure 1, this time one which is not plane (it has an accidental crossing but it can be redrawn without this crossing), but whose symmetry reveals information:

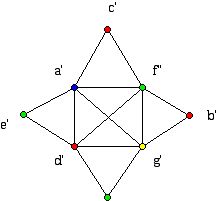
The four vertices a', d', f' and g' are each joined to the other three, showing that this graph has a clique of size 4 (e.g. complete subgraph of size 4), which means that the chromatic number must be at least 4. Since we saw the graph is indeed planar, we know there must be a four-coloring of the vertices. There are, in fact, many four colorings of this graph. Unfortunately, the one above does not use each of the colors equally often. With greater care for this particular example we can achieve our second goal of not only finding a coloring using the chromatic number of colors but of using each color equally often!

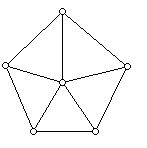
In general, one can not be sure that the number of vertices of the graph one is seeking to color will be divisible by the chromatic number for the graph. Thus, it may not be possible to achieve a coloring with a minimal number of colors where each color is used equally often. Even when the chromatic number does divide the number of vertices of the graph being colored, one may not be able to achieve a coloring where each color is used equally often.

The graph above has (vertex) chromatic number three but there is no coloring of the graph which uses each color twice.

3. Resolving conflicts (II)

We have seen how, using a graph coloring model, we can assist in the scheduling of committees to avoid having members of the committees being scheduled to be in two places at one time in the minimum number of time slots. Just as in "theoretical" mathematics, mathematicians seek ways to generalize or specialize results that they have proven in the area of applications of mathematics; success with solving a problem in one situation encourages one to try to solve similar problems in related situations.

What we need to look for is situations where we can use a graph model to represent objects and join two of these objects when we want to "avoid a conflict." Another example of this kind is in the scheduling of examinations at high schools and colleges. Our goal again is to avoid asking a student to be in a situation where he/she is being asked to take examinations for two different classes at the same time. Even modestly sized colleges offer very large numbers of courses and sections of courses. There are some practical considerations that in some cases it is desired that all the different sections of a course have a common final. However, graph-coloring models have proved to be valuable in practice here. Typically one might set in advance the number of time slots one wants to achieve and see if one can find a coloring of the conflict graph with this number of colors. If no solution exists, one might try to find a coloring that minimizes the number of conflicts, in some precisely definable sense.

Other examples of the way that coloring the vertices of a graph can be used to schedule or resolve conflict are:

a. Scheduling the use of tracks by railroads

b. Assigning radio frequencies

When radio stations are geographically too close in distance to each other and broadcast on the same or nearby frequencies they can interfere with each other. Draw a graph whose vertices are the stations and join them with an edge if they are are within a certain distance. Coloring the vertices of the graph where the colors correspond to frequencies gives an assignment where, when two stations get the same frequency, they will not interfere with each other.

c. Resource allocation

Suppose that there is a collection of basic tasks to perform which can be accomplished by allocating some of a set of m resources. The time it takes to perform a task is a fixed constant amount. Furthermore, we have the list for each task T_i of resources R_i that need to be assigned to get the task done. We construct a graph G as follows. For each task we create a vertex T_i and we join two tasks T_i and T_j by an edge whenever the lists R_i and R_j have at least one element in common. The reason for doing this is that we want to "tag" the fact that we can not do T_i and T_j at the same time because they need overlapping resource allocations. A coloring of the graph assures that tasks which get the same color can be performed simultaneously because the resources for them are simultaneously available. The shortest (total) time to get the tasks done will be accomplished when we have colored the vertices of the graph with the chromatic number of colors for the graph.

d. Zoos and pet stores

A pet store (zoo) wants to assign fish to acquaria (enclosures) so that fish (animals) that are not compatible (e.g. eat or attach each other) go into separate tanks (enclosures). For the pet store setting, if we create a vertex of a graph H for each species of fish and join two vertices if the species they represent are compatible, then finding the chromatic number of the resulting graph will give the most "efficient" way to store the fish.

4. From schoolgirls to tournaments

The following problem has come to be called the Lucas' (1842-1891) Schoolgirls Problem. Lucas is best known for his posing of the Tower of Hanoi Problem (1883). Consider the situation one sometimes sees in primary schools where on assembly day, students line up in pairs and walk into the auditorium in rows of two students each. Given an even number (2s) of students who take a walk in pairs, what is the largest number of days they can take such walks so that no pair of girls walks together on more than one day? This problem can be solved by thinking about the complete graph on an even number 2s of vertices, K_2s. This is the graph where one has 2s vertices each joined to every other one. It is not difficult to see that a coloring of the edges of this graph matches pairs of students and that one gets a different matching corresponding to each of the colors in an edge coloring with a minimal number of colors. Thus, since K_2s = 2s - 1, one can have 2s girls walk in pairs without a repeat for 2s - 1 days.

What is the chromatic index, the minimum number of colors to color the edges of a graph, for a complete graph with n vertices? The answer depends on whether n is even or odd:

When n is odd the chromatic index of the complete graph on n vertices is n;
When n is even the chromatic index of the complete graph on n vertices is n - 1.

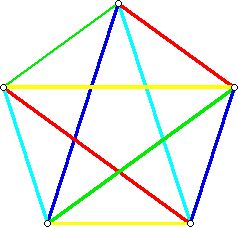
The way to construct a coloring can be seen by generalizing what is done for the example of n =5 (odd) and n = 6. One begins by drawing a regular n-gon, n odd, and forming a complete graph by adding the necessary edges. Now one uses n colors to color the boundary of the regular n-gon and and, for a fixed edge on the boundary, colors all of the other edges parallel to the edge in the complete graph the same color as shown below:

To handle the case of an even number of vertices, add a vertex to the coloring for the odd number with one less vertex, and color the extra edges as shown below:

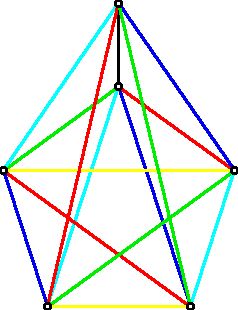
For the 6 students represented in the diagram above, they can walk in pairs for 5 days. On day one have the pairs matched by the blue edges walk together, on day two have the pairs matched by the red edges walk together, etc. This construction can be generalized for any odd value of n, and, thus, for any even value of n. However, once we see that the Lucas problem can be solved by finding the chromatic index of a complete graph, we realize that we can apply what we have seen to a different, perhaps more common situation,.

The discussion above shows how to design a round robin tournament for an even or odd number of players, and conduct the tournament in a minimum number of rounds. The goal in a round robin tournament is to have each team (player) play every other team exactly once. For an even number of teams 2s, one needs 2s - 1 rounds, where in each round the teams with the same edge color are paired, while when there are an odd number of teams there will be n (=2s-1) rounds, where in each round one team gets a "bye" (i.e. the team with a bye does not play that round) and the teams that play a given round are those paired by edges with the same color.

Another simple-to-state result that was first demonstrated without any applications context was discovered in 1916 by Denes König (1884-1844), and has proved to be significant in applied coloring problems.


The result states that if G is a graph (several edges between a pair of vertices being allowed) whose vertices can be colored with two colors (bipartite graph), then the minimum number of colors to color the edges of G is equal to the maximum valence of any vertex in the graph.

For example, the graph below shows a bipartite graph with maximal valence three, and which has been three edge colored. Although the graph below has all its vertices having the same valence this is not necessary for König's Theorem to apply.

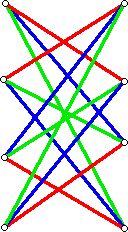
Recent ideas involving the design of optical communications networks have led to a variety of new edge coloring problems (see Peter Winkler's abstract) including conjectured generalizations of König's Theorem.

5. Mathematics and cell phones

Mathematics has played an increasingly large role in the development of new technologies. Examples include the use of mathematical techniques for error-correction and data-compression technologies that are involved in the use of audio and video compact discs. Among the most visible of new technologies, which is dramatically changing the way people interact and communicate with each other, is the emergence of cheap and increasingly reliable cell phone service. Error-correction and data compression codes play an indirect role in making cell phone service possible. There is hardly a branch mathematics that has not played some part in bring cell phone technology to its current ubiquitous status. As a simple example which does not involve issues of coloring, consider the problem of providing cell phone service in a region that currently has none. What is required is to divide the region up into cells to serve the people within that region. At one extreme one can have one cell for the whole region and at the other extreme many small cells. What are the tradeoffs between these two approaches? Mathematics helps sort out when one approach is better than the other.

When you place a cell phone call, the phone must send out an electronic signal which carries a digitalized version of your speech. This signal must be sent at a frequency which will not interfere with the calls that are being placed by other nearby users of cell phones, otherwise there will a degradation of the signal quality or in the worst case a "dropped call." This refers to a call which has been connected and where a person is speaking to his/her desired party, but during the course of the conversion there is a loss of signal which disconnects the call. Cell phones make use of radio signals. We take the use of radio so for granted that it's hard to realize that "commercial use" of radio is only about 100 years old. Marconi won the 1909 Nobel Prize in Physics for his work on "wireless telegraphy." Today, the bands used for communication are: VLF (very low frequency), LF (low frequency), MF (medium frequency), HF (high frequency) VHF (very high frequency), UHF (ultra high frequency) SHF (super high frequency) and EHF (extreme high frequency). The applications which are supported include radio, television, maritime communication and navigation, global positioning systems, space communication, military and police communications, microwave transmissions, radio astronomy, and radar, to mention but a few.

Over a period of time, as often happens in applied problems, relatively simple ways used to deal with constructing a mathematical model for the cell phone situation have been replaced by more complex approaches that are more realistic. We saw (in Section 4) a way to use graph coloring to assign radio frequencies in a very simple environment. Here is a description of the issues that a more elaborate mathematical model attempts to address. When a cell phone user wishes to make a call, a frequency (or channel) must be used to carry the call on. If this frequency is the same or too close to the frequency being used to carry another user's call, there will interference or in a sufficiently bad case, the call will be "dropped." One of the techniques used to deal with cell phone traffic problems of this kind was introduced by W. Hale, approximately 25 years ago.

We are given a set of transmitters which are to be assigned one of an available collection of equally spaced frequencies which are numbered from 0 to n. These frequencies are thought of as colors, and each user is represented by a vertex of a graph. Two vertices (transmitters) are joined by an edge when the transmitters they represent must get different frequencies. For a given transmitter u, the color assigned to it will be denoted f_u. When one has assigned frequencies to the vertices, since these frequencies are non-negative integers, we can think of there being a distance associated with two transmitters whose vertices are joined by an edge. This distance is the difference (computed so that one gets a non-negative number) in the frequencies which are assigned to them. The prohibited distances can be the same for all edges or can vary from edge to edge. For the edge from v to w the prohibited set of frequencies will be denoted T_vw. Thus, the assignment rule f for colors is required to obey |f_v - f_w| œ T_vw. We always insist, for every edge, that 0 be a member of the prohibited set for that edge. This condition forces vertices joined by an edge to have different colors. A coloring which obeys these rules is known as a T-coloring. The minimum number of colors used in a T-coloring is denoted by c_T. A theorem of M. Cozzens and F. Roberts shows that for a graph G, c_T(G) = c(G). Thus, perhaps surprisingly, from the perspective of the number of colors needed, one is not "hurt" by having more constraints on assigning colors to the vertices. However, there is another optimization condition that can be considered for the T-coloring environment. The span of a T-coloring is the difference between the largest and smallest color number used in coloring the vertices of the graph. There are simple examples for which there is no coloring that uses the smallest number of colors and simultaneously achieves the smallest span. Further generalizations of this basic framework expand the idea of a T-coloring to a list T-coloring. Here the idea is that there are "blocked" frequencies which can not be assigned to a vertex, so that in trying to achieve a coloring one must limit the choice at each vertex to a list of non-blocked colors (frequencies). As mathematical techniques are found to solve these more general coloring problems, attempts are made to "up the ante" and solve even more complex ones. Sometimes it possible to show that the problems one is concerned about solving in the real world are so hard (i..e. NP-complete) that no fast algorithm is likely to be found to solve them. New ideas and approaches to using coloring to solve applied problems are being regularly investigated. As we so often see, mathematical ideas and appications of mathematics grow in tandem.



6. References

Appel, K. and W. Haken, Every Planar Map is Four Colorable, American Mathematical Society, Providence, 1989.

Bodendiek, R. (ed.), Graphen in Forschung und Unterricht, Festschrift K. Wagner, Dad Salzdetfurth: Barbara Franzbecker.

Bogart, K., Discrete Mathematics, Heath, Lexington, MA., 1988.

Borodin, O., On cyclic coloring of planar graphs, Discrete Math., 100 (1992) 281-289.

Borodin, O., Cyclic degree and cyclic colorings of 3-polytopes, J. of Graph Theory, 23 (1996) 225-231.

Borodin, O., Structural theorem on plane graphs with application to the entire coloring number, J. of Graph Theory, 23 (1996) 233-239.

Brightwell, G., Partial Orders, in Graph Connections, L. Beineke and R. Wilson, (eds.), Oxford Press, Oxford, 1997, pp. 52-69.

Cozzens, M. and F. Roberts, T-colorings of graphs and the channel assignment problem, Congr. Numer. 35 (1982) 191-208.

Cozzens, M. and D.-I. Wang, The general channel assignment problem, Congr. Numer. 41 (1984) 115-129.

Diestel, R., Graph Theory, Springer-Verlag, New York, 1997.

Dirac, G., Percy John Heawood, J. London Math. Soc., 38 (1963) 263-277.

Fiorini, S. and R. Wilson, Edge-colourings of Graphs, Research Notes in Mathematics, Vol. 16, Pitman, 1977.

Fritsch, R. and G. Fritsch, The Four-Color Theorem, Springer-Verlag, New York, 1998.

Grünbaum, B., Convex Polytopes, Wiley-Interscience, New York, 1967. (Second edition, 2003.)

Gutner, S., The complexity of planar graph choosability, Discrete Math., 159 (1996) 119-130.

Hadwiger, H., Über eine Klassifikation der Streckenkomplexe, Vierteljahrschriften der Naturforschungsgesellschaft Zürich, 88 (1943) 133-142.

Hale, W., Frequency assignment: theory and applications, Proc. IEEE 68 (1980) 1497-1514.

Hale, W., Frequency assignment methodology: an annotated bibliography, NTIA-SP-80-10, N.T.I.A., Institute for Telecommunication Sciences, Boulder, CO, 1980.

Hartsfield, N. and G. Ringel, Pearls in Graph Theory, Revised and Augmented Edition, Academic Press, Boston, 1994.

Heesch, H., Zur systematischen Strukturtheorie III, IV, Z. Krist. 73 (1930) 325-345, 346-356.

Heesch, H., Untersuchungen zum Vierfarbenproblem, Mannheim/Wien/Zürich, Bibliographisches Institute, 1969.

Heesch, H., E-Reduktion, Preprint Nr. 19 des Instituts für Mathematik der Technischen Universität Hanover. (Also, in Bodendiek, Festschrift, Klaus Wagner.)

Jensen, T. and B. Toft, Graph Coloring Problems, Wiley, New York, 1995.

Kronk, H., and J. Mitchem, The entire chromatic number of a normal graph is at most seven, Bull. Amer. Math. Soc., 78 (1972) 799-800.

Kronk, H. and J. Mitchem, A seven-color theorem on the sphere, Discrete Math., 5 (1973) 255-260.

Lebesgue, H., Quelques consequences simple de la formule d'Euler, J. de Math. Pures et Appl., 19 (1940) 27-43.

Malkevitch, J., Convex isosceles triangle polyhedra, Geombinatorics 10 (2001) 122-132.

May, K., The origin of the four-colour conjecture, Isis, 56 (1965) 346-348.

Mirzakhani, M., A small non-4-choosable planar graph, Bull. Inst. Combin. Appl., 17 (1996) 15-18.

Mohar, B. and C. Thomassen, Graphs on Surfaces, John Hopkins University Press, Baltimore, 2001.

Opsut, R. and F. Roberts, On the fleet maintenance, mobile radio frequency, task assignment, and traffic phasing, in G. Chartrand, Y. Alavi, D. Goldsmith, L. Lesniak-Foster, and D. Lick, (eds.), The Theory and Applications of Graphs, Wiley, New York, 1981, pp. 479-492.

Ore, O. The Four Color Problem, Academic Press, New York, 1967.

Plummer, M. and B. Toft, Cyclic coloration of 3-polytopes, J. Graph Theory, 11 (1987) 507-515.

Ringel, G., Färbungsprobleme auf Flächen und Graphen, VEB Deutscher Verlag der Wissenschaften, 1959.

Ringel, G. Map Color Theorem, Springer-Verlag, New York, 1974.

Ringel, G., 250 Jahre Graphentheorie, In: Graphen in Forschung und Unterricht: Festschrift K. Wagner, Barbara Franzbecker Verlag, 1985, pp. 136-152.

Roberts, F., T-colorings of graphs: recent results and open problems, Discrete Math. 93 (1991) 229-245.

Robertson, N., and D. Sanders, P. Seymour, R. Thomas, The four color theorem, J. Combinatorial Theory Ser. B. 70 (1997) 2-44.

Robertson, N., and D. Sanders, P. Seymour, R. Thomas, Every 2-connected cubic graph with no Petersen minor is 3-edge colorable. (To appear.)

Robertson, N. and P. Seymour, Graph minors - a survey. Surveys in Combinatorics, 1985, London Math. Soc. Lecture Note Series, Volume 103, Cambridge U. Press, Cambridge, p. 153-171.

Robertson, N. and P. Seymour, R. Thomas, Hadwiger's conjecture for K₆ - free graphs, Combinatorica, 13 (1993) 279-361.

Saaty, T. and P. Kainen, The Four-Color Problem: Assaults and Conquest, McGraw Hill, New York, 1977.

Sanders, D. and Y. Zhao, On simultaneous edge-face colorings of plane graphs, Combinatorica, 17 (1997) 441-445.

Sanders, D. and Y. Zhao, On total 9-coloring planar graphs of maximum degree seven, J. Graph Theory, 31 (1999) 63-73.

Sanders, D. and Y. Zhao, On the entire coloring conjecture, Canad. Math. Bull., 43 (2000) 104-114.

Schnyder, W., Planar graphs and poset dimension, Order 5 (1989) 333-343.

Schnyder, W., Embedding planar graphs on the grid. Proc. First ACM-SIAM Symposium on Discrete Algorithms, (SODA), 1990, pp. 138-148.

Schnyder, W. and W. Trotter, Convex embeddings of 3-connected plane graphs, Abstracts AMS, 92T-05-135, 1992.

Tesman, B., T-colorings, list T-colorings, and set T-colorings of graphs, PH.D., Thesis, Department of Mathematics, Rutgers University, New Brunswick, October, 1989.

Tesman, B., Applications of forbidden difference graphs to T-coloring, Congr. Numer. 74 (1990) 15-24.

Tesman, B., set T-colorings, Congr. Numer. 77 (1990) 229-242.

Thomassen, C., Every planar graph is 5-choosable, J. Comb. Theory B, 62 1994) 180-181.

Thomassen, C., Grötzsch's 3-color theorem, J. Comb. Theory B, 62 (1994) 268-279.

Thomassen, C., 3-list coloring planar graphs of girth 5, J. Comb. Theory B, 64 (1995) 101-107.

Voigt, M., List colourings of planar graphs, Discrete Math., 120 (1993) 215-219.

Voigt, M. and B. Wirth, On 3-colorable non-4-choosable planar graphs, J. Graph Theory, 24 (1997) 233-235.

Wagner, K., Über zwei Sätze der Topologie: Jordanscher Kurvensatz und Vierfarbenproblem, Doctoral Dissertation, Köln; supervisor, Karl Dörge, 1935.

Wagner, K., Bemerkungen zum Vierfarbenproblem, Jahresber. Deutsch. Math. Verein., 46 (Pt. 1) (1936) 26-32.

Wagner, K., Ein Satz über Komplexe, Jahresber. Deut. Math. Verein., 46 (Pt. 2) (1936) 21-22.

Wagner, K., Zwei Bermerkungen über Komplexe, Math. Annalen, 112 (1936) 316-321.

Wagner, K., Über eine Eigenschaft der ebenen Komplexe, Math. Annalen, 114 (1937) 570-590.

Wagner, K., Über eine Erweiterung eines Satzes von Kuratowski, Deutsche Math., 2 (1937) 280-280.

Wagner, K., Bermerkungen zu Hadwigers Vermutung, Math. Annalen, 141 (1960) 433-451.

Wagner, K. Beweis eine Abschwächung der Hadwiger-Vermutung, Math. Annalen, 153 (1964) 139-141.

Waller, Simultaneously colouring the edges and faces of plane graphs, J. Combin. Theory B, 69 (1997) 219-221.

Wang, D.-I., The channel assignment problem and closed neighborhood containment graphs, Ph.D. Thesis, Northeastern U., Boston, MA., 1985.

West, D., Introduction to Graph Theory, Second Edition, Prentice-Hall, Upper Saddle River, 2001.

Wilson, R., Graphs Colourings and the Four-colour Theorem, Oxford, Oxford, 2002.

Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet can be used to get additional bibliographic information and reviews of some of these materials.