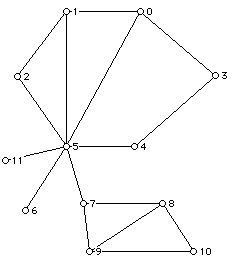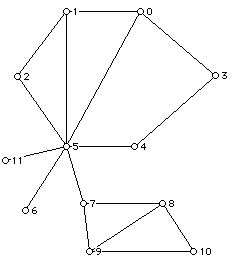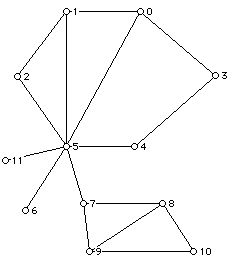
Figure 1
Geometric Structures (Sample Final, Spring, 2008)
Final Examination
Prepared by:
Joseph Malkevitch
Department of Mathematics
York College (CUNY)
Jamaica, New York 11451
email:
malkevitch@york.cuny.edu
web page:
http://york.cuny.edu/~malk/
Show all work in blue book.
Have fun and good luck!
1. (36 points) Draw a diagram which illustrates:
a. A rhombus which is not a square
b. A regular convex octagon.
c. A connected planar but not plane graph with 6 vertices and no circuits.
d. A convex plane quadrilateral which corresponds to the side length partition {2, 1, 1} and angle measure partition {2, 1, 1}.
e. A trapezoid with three equal sides that is not a rectangle
f. An equiangular hexagon which is not a regular hexagon
2. In the real projective plane:
(10 points)
a. Find the equation of the line which joins the points:
i. (-4, 0, 2) and (-2, 0, 0)
ii. (3, 2, 1) and (-4, 3, 2)
(10 points)
b. Find the point of intersection of the lines
i. 2x -3y + z = 0 and y = 0
ii. -x + y - 2z = 0 and 2x -y - z = 0
3. Consider the finite affine geometry (plane) of order 3 whose points are pairs (x, y) from Z3 (the integers mod 3) and lines are of the form ax + by + c = 0.
(20 points)
a. Write down all of the lines which go through (2, 1)
b. List all of the points on the line x + y = 2.
c. Find the line through (2, 1) and (1, 2)
d. Find the line through (1,1) parallel to the line 2x + y = 1
e. In the projective plane associated with this plane, find all of the points on the line x + 2y = 0
4.
(9 points)
a. Determine the values of vi, the number of vertices with valence i for the graph below and determine the values of pi, the number of faces with i sides for the graph below.
(5 points)
b. What is the vertex coloring number for the graph below (Figure 1)?
(5 points)
c. What is the face coloring number for the graph below (Figure 1)?

5. (5 points)
a. Draw a diagram which will serve as a model for a finite projective plane.
b. What is the minimum number of edges required to eulerize the graph in Figure 1.
c. What is the number of edges in a minimum cardinality walk which traverses each edge of Figure 1 at least once and starts and ends at vertex 3?
d. Give a precise statement of Steinitz's Theorem which gives necessary and sufficient conditions for when a graph (with no loops or multiple edges) is the vertex-edge graph of a convex 3-dimensional polyhedron.
e. Determine the set of points which are equidistant from (-10, 2) and (6, 4) in the taxicab plane. (Describe this set using one or more equations.)
Have a great summer!
Name: