Prepared by:
Joseph Malkevitch
Department of Mathematics
York College (CUNY)
Jamaica, New York 11451
email:
malkevitch@york.cuny.edu
web page:
http://york.cuny.edu/~malk/

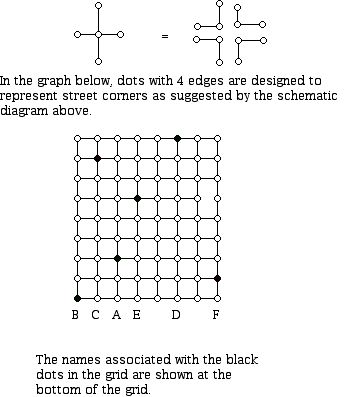
Let us consider several problems, all of which will use as "input data" the diagram above.
Situation 0:
A contractor located at B has been hired to check the streets in the urban area shown above for pot holes. All the street segments shown will take the same time to traverse. The contractor wishes to traverse (walk) each segment of street at least once and return to B, following a route which will minimize the total amount of time for the inspection. What is this minimum amount of time?
(As part of your solution, explain why it is not possible to traverse each section of street once and only once on a tour that starts and ends at B.)
Situation 1:
You live at A and must run errands by foot that take you to the sites B, C, D, E, and F in any order you might want, and then return to A. What route makes the most sense? How far do you have to walk to achieve your "best" result? Are there different routes that are "best," and if so how many are there?
Situation 2:
A company must lay cable to connect up the sites A, ..., F so that messages can be sent between any pair of sites by relay if necessary. Thus, if cable is laid from A to B and B to C, cable does not have to be laid between A and C because one can relay a signal from A to C via B. If the cost of laying cable is proportional to the "distance" between two sites, what site pairs should be joined to minimize the cost of providing the cable service between the sites?
Situation 3:
Students live at sites A, ..., F. A teacher wishes to group the students in pairs for the purposes of working on projects. If X and Y are paired it is assumed that X will walk to Y's house or the other way around to work together. What pairing will minimize the "average" distance that must be walked to have the students work together?
Situation 4:
There are apartment blocks (or single family homes at A,...,F. Where would would an optimal location to place mobile medical facility which would:
a. Minimize the maximum distance that it would take to reach the mobile facility.
b. Minimize the total distance from all of the locations (A-F) to reach the mobile medical facility.
Situation 5
Which points (with coordinates which may or may not be integers) are closer to point E than any of the other point represented by dark dots, and, thus, could be served by a post-office at E?
Situation 6
Is it possible to assign a direction to each small horizontal and vertical segment in the diagram above so that for any pair of dots P and Q in the diagram one can drive from P to Q and then back from Q to P obeying the directions of the arrows?
--------------------------------------------------------------------------------------------------------------
For each of the Situations 0, 1, 2, 3, 4, 5 and 6 above, give as many examples of "real world situations" as you can which seem to you to be similar to these.
Suppose you have described a group of problems which which appear to you to be similar to Situation 1. Now for each of these problems explain how you think the problem is like Situation 1 and how you think it differs from Situation 1. Carry out this same process for the problems you found similar to Situation 0, 2, 3, 4, 5 and to Situation 6.
Make up a new problem of your own invention based on the diagram and information implicit in the diagram given at the start. Perhaps you may want to ask that more information be added to the diagram to make up your problem. For example, you might want to know if there are traffic lights at any of the corners, or in what directions the automobile traffic can move on the streets shown.
The material above was originally developed for a workshop given at Teachers College at Columbia, entitled Mathematics, Politics, and Society (July, 2004) Further work was supported in part by the Teacher Academy of York College. Specific funding was provided by: FIPSE (46274-07 01) and the Fund for PS (72042-07 01) to the Teacher Academy of CUNY. Additional evolution of the material has occurred due to presentation in other settings.