Thematic Approaches to Mathematical Modeling (2017)

Prepared by:

Joseph Malkevitch
Department of Mathematics
York College (CUNY)
Jamaica, New York 11451

email:

malkevitch@york.cuny.edu

web page:

http://york.cuny.edu/~malk

In subjects outside of mathematics (as well as in mathematics courses) at the college level it is often helpful to have examples that show the power of mathematical thinking. Sometimes this is done by asking for examples to respond to student questions of the kind: When can the fact that I can solve a linear equation help me in political science or business? The same style of question arises for the full range of mathematical techniques (percents, quadratic equations, slope, etc.). Here, bigger picture reasons for studying mathematics are offered with examples.

1. Optimization

a. Construction scheduling

Example: At a construction site for a new hospital many workers carry out tasks to get the hospital built as quickly as possible - time is money. A foundation has to be laid, a superstructure assembled, cement poured, electrical and plumbing systems installed, etc. Some of these tasks must be done before others, while some of the tasks can go on simultaneously. Mathematics enables the construction of a schedule which locates which task are critical from the point of view that any slippage in doing these tasks causes the whole project to be delayed, while other tasks have flexibility to some extent in how they can be scheduled without increasing the total project time.

Similar ideas can also be used to minimize the turn around time for a plane which has just arrived to leave on the next leg of its flight plan.

Mathematics: graph theory, early start-early finish; late start-late finish calculations; critical path method

b. Pot hole inspection

Example: After the winter many urban streets develop potholes. In order to efficiently repair these a survey first must be made to determine their location. Mathematically, this question, of efficiently surveying streets for pot holes, is similar to what must be done to deliver mail, remove snow, paint lane lines, pick up garbage, and design street sweeping routes.

Mathematics: graph theory; Euler's traversability theorem; Chinese postman model.

c. Matching workers and jobs

Example: A small company has a core collection of workers (jacks of all trades) and various jobs within the company they might carry out. Each worker gets a certain satisfaction from doing a particular job and has a time that it takes him/her to do it. When is it possible to assign workers to jobs they are qualified for? What assignment minimizes the time to get the jobs done? What assignment optimizes worker satisfaction?

Mathematics: graph matchings; bipartite matchings; Philip Hall's Marriage Theorem; alternating path algorithm.

2. Growth and Change

a. Credit card management

Example:

If you buy a new large screen TV for $1000 with a credit card and pay off the minimum amount required each month, how long will it take you to repay your loan? How much money will it cost to buy your TV if you proceed in this way? The answer depends on the card's interest rate and the bank's policy about minimum payments.

Mathematics: Difference equations; logarithms, half-life. Percentages.

b. Salary management

Example:

Your boss offers you a choice of having your salary go up by $1000 a year for the next five years or going up by 4% a year for five years. Which is a better offer?

Mathematics: Linear functions; exponential functions, mathematical models.

3. Information

a. Scratches on a DVD or CD

Example: Why do DVD's and CD's continue to play properly even when they have scratches or smudges on them? The answer lies in the development of error correction technologies which allow a system for coding the information on the DVD or CD to correct errors due to noise (dust, smudges). Data sent from the International Space Station, a space probe, or generated in computer calculations can also be protected by error correction ideas.

Mathematics: Error correction codes; Hamming distance.

b. Very small appliances

Example: How can a device as small as an iPod store so much music? How can I now watch more and more digital channels on television? Data compression technologies are often used in tandem with error correction systems. DVD's, CD's, cell phones, and HDTV typically incorporate both error correction and data compression systems. These data compression systems, together with engineering of smaller and smaller storage devices, make many new technologies possible.

Mathematics: Huffman trees; data compression.

4. Fairness and Equity

a. Bankruptcy

Example: A company with remaining assets of $210, 000 goes belly up. There are three creditors with verifiable claims of $180,000, $150,000, and $60,000. What is a fair way of paying off the claimants? Problems such as these actually are discussed in documents which are over 800 years old (Babylonian Talmud). The same mathematics which applies to bankruptcy settlements can be used in designing tax systems and settling estates.

Mathematics: Fairness axioms, game theory, constrained optimization.

b. School assignment

Example: Many urban school districts no longer insist that students attend a neighborhood school. Students are given choice, within certain parameters, of applying to a variety of schools. The schools also have interests in particular students. Given rankings for the students of the schools and the schools of the students is there a way to assign students to schools that is "fair" and where no school (S) -student (P) pair will "fall apart" because there is some school who would prefer P to the student it was assigned (and P prefers that school) or there is some student who would prefer S to the school he/she was assigned (and that S would prefer that student)? Problems of this kind also arise in kidney transplant schemes and hospitals finding resident doctors when they finish medical school.

Mathematics: Gale-Shapley model; Game theory; preference relations; two-sided markets.

5. Risk

a. Plane travel versus car travel

Example: Many people are fearful of flying on a commercial flight but will get into an automobile with a neighbor who has had one or two drinks. Which is riskier?

b. Decision making; probability models.

Examples: Given complicated choices, how can we help a decision maker choose the best one? One issue that must be addressed is estimating the probabilities of the different things that might happen. Often decision makers can provide "utilities" which enable them to compare the trade-offs between the results of the decisions which they make. Utilities might be used to try to quantify to what extent one would rather have a vacation in Mexico versus one in Egypt. One can then make decisions which maximize expected utility. Similar ideas can be used to try to distribute shared properties when couples separate during a divorce.

Mathematics: Game theory, utility theory, fair division algorithms.

c. Heath care

How risky is it to take vitamins with artifical red dye every day for 20 years? Is the risk of getting cancer from CT scans, mamograms, and dental x-rays worth the risk?

Mathematics: Probability modeling; utility.

6. Shape and Space

a. What is the "shape" of the universe?

Example: Does our universe go on forever or is it like the surface of a sphere, such that if one travels long enough in the same direction one returns to where one started? The answer is we do not know but mathematicians and physicists are designing experiments, conducting observations, and developing ideas to help decide what is truly the case.

Mathematics: Euclidean, projective, and hyperbolic geometry.

b. Packaging

Example: When you get a present in a cardboard box, the box began its life as something flat that got folded and assembled into a box. If the box is a perfect cube, how many different shapes will fold into this cube? It turns out there are 11 such patterns, but these patterns can also be folded into shapes other than cubes.

Mathematics: Alexandrov's Theorem; folding and unfolding algorithms.

7. Pattern and Symmetry

a. Fashion design

Example: We see a very wide range of patterns in the clothes that we and others wear. However, if the pattern is symmetric in certain ways, then the number of different types of patterns is very limited. Thus, on a strip there are only 7 different types of symmetric patterns where a "motif" has been replicated along the strip. There are 17 types of symmetrical wall paper.

b. Sorting mail

Example: The US Postal Service delivers huge volumes of mail. The use of machine readable binary codes helps with speeding up this process. In addition, to read these codes it is helpful to have machines place the letters in a standard position to enable the reading of the codes. One way to do this is to search for the stamp, which is located in the upper right corner of an envelope. What is an efficient way to take an envelope and make sure that the letter is "face up" with the stamp in the upper right corner?

Mathematics: geometric transformations; binary codes, group theory.

8. Order and Disorder

a. Mutual friends or strangers

Example: You are at a meeting of 6 people. There must be at least three people who already mutually know each other or there are at least three mutual strangers.

Mathematics: Ramsey's Theorem.

b. Deterministic systems can look like noisy systems

Example: A deterministic system is used to model a viral epidemic to see what might happen as the epidemic progresses. However, very small changes in the data about how the system is initialized dramatically affect the scenario of what happens. We expect noisy systems to be "unpredictable" but many "deterministic" systems are also unpredictable.

Mathematics: Chaos, difference equations, dynamical systems.

9. Reconstruction (from partial information)

a. Sampling

Example: A relatively small sample randomly selected from a population can be used to get very accurate information about the population.

Mathematics: Mean, standard deviation, sampling distribution of the mean.

b. Origins of a disease

Example: Where did AIDS come from and how did the disease progress? Using virus samples that date back from the period when the nature of AIDS was not understood, we can try to paint a picture of how the disease progressed. This is done by defining measures to tell how far apart two different strains of a virus are, and then using a system to cluster viruses which are close into groups.

Mathematics: distance matrices; phylogenetic trees, cluster analysis, data mining.

10. Conflict and Cooperation

a. European harmony

Example: As the European Union has expanded to allow the entry of additional countries into the Union, new governance arrangements must be made. A country such as Luxembourg, though a member of the EU, is not as powerful politically or economically as Spain, Germany, France, England or Italy. To deal with these issues countries are assigned weights and votes are based on a weighted voting system.

Mathematics: game theory; weighted voting; power indices, social choice theory.

b. Self-enforcing agreements

Example: Concern about global climate has been growing. Proposals have been made to have countries limit the amount of pollutants and other gases that are released into the atmosphere. How can such agreements be made to work? One approach is to make arrangements where cooperation in carrying out the agreements encourages compliance by offering benefits to those countries which cooperate. In fact, those who do not comply will only hurt themselves.

Mathematics: Game theory; mechanism design.

11. Similarity and Dissimilarity

a. Development of new drugs

Example: How does one discover safer and more effective drugs? One approach is to take molecules which have useful features or are known to be chemically active in promising ways, and modify them so as to make them less toxic or combine features to create a synergy. This approach requires being able to finds ways of measuring "distance" between two molecules.

Mathematics: Distance matrices; Hamming distance; edit distance.

b. Homeland security

Example: To increase security at airports it is necessary to have software that will reliably tell one person from another. If there is a way of associating a collection of numbers with a face, then one can tell two faces apart by comparing the numbers associated with the two different faces. When the "distance" between the two faces is large enough, it is assumed they are different people.

Mathematics: Edit distance; Hamming distance.

c. Scale comparisons and index design

Example: How can one compare whether one food is "hotter" (more spicy) than another? How can one compare hurricanes in terms of how destructive one might think they could be? This involves the creation of an appropriate index or scale on which to make comparisons. Other examples involve using mathematics to compare the strength of earthquakes or the rate of inflation from one month to the next. Students are often asked to answer questions about the effectiveness of their teachers. Is it meaningful to add the numbers that a class of students produce to get a "class mean?"

Mathematics: Measurement theory; statistics.

12. Close Together and Far Apart

a. Spell checkers

Example: When people type documents on a computer, they often make typographical errors. Such errors are found by checking if the typed word is in a "dictionary" which is previously stored on the computer. When a word is not in this dictionary a spell checker suggests words that the person who was typing might have meant. These suggested words are made on the basis of:

i. A "legal word" in the dictionary that differs from the typed word in a minor way. ("Zad" was typed but had, bad, mad, lad, sad, etc. might have been meant.)

ii. A word that sounds like the word that was typed. Some errors occur because the typist spells something phonetically but the chosen spelling is not legal. ("Trofy" was typed but the person meant trophy.)

Mathematics: Hamming distance; edit distance; systems for coding words that sound alike.

13. Unintuitive behavior

a. Urban Traffic

Example: The transportation department proudly announces that a road under construction for 10 years has finally been completed. One reason for building the road is to cut down on congestion. However, after opening the new road conditions become worse.

Mathematics: Braess' paradox; game theory.

b. Scheduling

Example: After many complaints that the tasks being worked on by some machines are not getting done quickly enough, a decision is made to add another processor to work on the tasks. Yet, instead of getting things done more quickly, the tasks take even longer to be completed.

Mathematics: Scheduling algorithms; graph theory; bin packing models.

---------------------------------------------------------------------------------------------------------
Examples of a sample of "mathematical playgrounds."

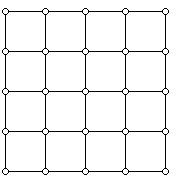
1. A model of a small section of a city is shown below. The roads involved are two-way, and a pothole inspector who goes down a street section can inspect for potholes in the lanes in either direction. If the inspector starts at the upper left hand corner, what is the shortest length (in terms of number of blocks) route that can be designed so that each block section is inspected at least once? Here the grid is a "square" but one could look at a similar problem in a "rectangular" environment.

The software will generate similar small grids and students can be led to a conjecture about what the shortest route for an mxn grid would be. The example above shows a 4x4 grid.

2. A student will be able to work with a "credit card" calculator. By entering an interest rate, payment amounts, size of purchase, etc., comparisons can be made for how long it will take to repay what is borrowed and what the total cost of doing the borrowing would be.

3. For sizes of remaining assets E (estate size) and different claims, a comparison can be made as to how different approaches to settling bankruptcy problems distribute the remaining assets.

Bibliography:

Brams, S., Mathematics and Democracy, Princeton U. Press, Princeton, 2008.

COMAP, For All Practical Purposes (10th edition), W.H. Freeman, New York, 2016.

Jones, N. and P. Pevzner, An Introduction to Bioinformatics Algorithms, MIT Press, Cambridge, 2004.

Tannenbaum, P., Excursions in Modern Mathematics (7th edition), Prentice-Hall, New York, 2010.

Taylor, A. and A. Pacelli, (2nd edition) Mathematics and Politics, Springer-Verlag, New York, 2008.

H. Young, Equity in Theory and Practice, Princeton U. Press, Princeton, 1994.