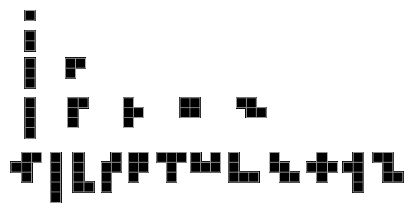
Figure 1
Polyomino Primer
Prepared by:
Joseph Malkevitch
Department of Mathematics and Computer Studies
York College (CUNY)
Jamaica, New York
email:
malkevitch@york.cuny.edu
web page:
http://york.cuny.edu/~malk/
A polyomino is a plane collection of 1x1 squares that are pasted together along their edges. Pioneers in the mathematical study of these fascinating geometrical objects was carried out by Solomon Golomb and David Klarner. Figure 1 shows the inequivalent polyominoes for polyominoes with n cells, for n from 1 to 5. (The analogues of polyominoes for equilateral triangles are called polyiamonds and polyhexes.)
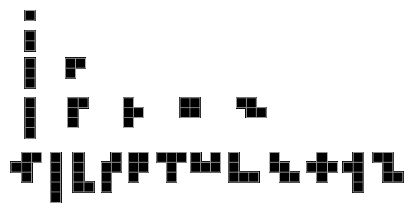
Sometimes it is convenient to think of a particular polyomino as as a rod structure and in other cases to think of as including the interior points of the cells which make up the polyomino. Sometimes it is convenient to think of a polyomino as a polygon and sometimes as a graph. Consider for example the polyomino with 4 cells in Figure 2.
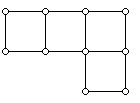
Treated as a graph, this polyomino has 10 vertices, 5 faces, 13 edges. All polyominoes are plane graphs but some of them are also outerplanar graphs. This means that all of the vertices lie on the unbounded face of the graph. The graph in Figure 2 is outerplanar while in Figure 5 the graph is not outerplanar. Note that as a graph the infinite or unbounded face of the graph is a 10-gon.
Figure 2 viewed as a polygon, it is sometimes convenient to think of it as a non-convex hexagon, with sides of lengths 3, 2, 1, 1, 2, 1. Thus, as a polygon we would say this polygon has perimeter 10. The polyomino consisting of 4 cells in a 2x2 square is equilateral because all of its sides thought of as having length 2.
Investigation 1
For which values of n is there a polyomino of n sides which is equilateral?
The example below (Figure 3) shows a polyomino with 12 sides which is equilateral!
A natural question is whether or not "holes" are allowed in a polyomino. Thus, if we have a 3x3 collection of 9 unit cells, we can omit the "center" cell and still have 8 cells which touch edge to edge. It is usual to allow this in a polyomino but here, unless stated otherwise, we will not allow polyominoes with holes. This is another example of setting "rules" or "choosing" definitions that lead to interesting and/or provable results.
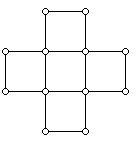
Although there are infinitely many polyominoes that can be regarded as convex polygons (all with 4 sides) polyominoes usually are non-convex when regarded as polygons. However, there is an intriguing idea which enables one to tell non-convex polyominoes apart, and which leads to some interesting questions. If one intersects the pentomino in Figure 4 with vertical lines the result is always a connected set. However, horizontal lines do not always cut the polygon with a connected set. The polyomino in Figure 4 is considered vertically convex but not horizontally convex.
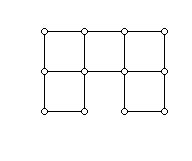
The polyomino in Figure 5 while not convex is vertically and horizontally convex. Notice that as a graph it has vertices which do not appear on the boundary of the polyomino.
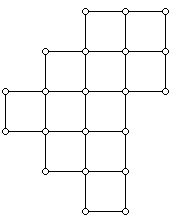
Among the many problems and issues that the study of polyominoes inspire are:
1. Which polyominoes will tile the plane?
2. Which sets of polyominoes will tile the plane?
3. There are 12 pentominoes so the whole set of these has area 60. This suggests the question of whether or not 3x20, 5x12, and 6x10 rectangles can be tiled with the twelve polyominoes.
4. Find a "formula" for the number of polyominoes? No such formula has been found but there are estimates for the number of inequivalent polyominoes with n cells.
5. Which polyominoes interpreted as graphs have Eulerian circuits and which ones have Hamiltonian circuits? (A Hamiltonian circuit in a graph is cycle that visits all the vertices, that is, a closed tour of the vertices that visits each vertex once and only once using distinct edges.) For example it is not a difficult exercise to show that there infinitely many polyominoes which have Eulerian circuits and infinitely many that lack Hamiltonian circuits.
6. The art gallery problem for polyominoes asks for the number of vertex guards that are sometimes necessary and always sufficient to see:
a. A polyomino with n-cells (no holes)
b. A polyomino with k sides (viewed as a polygon)
More generally, for a particular polyomino one can ask for an algorithm which finds the minimal number of vertex guards.
A guard g, at a boundary point of a polygon can "see" any interior point i of the polygon which does include exterior points of the polygon on the segment gi.
There are also variant problems for guarding where one thinks of the individual cells of the polyomino as "pixels." One can now talk about pixel guards, where the points visible from a pixel are those points of the polyomino which are visible from some point of the pixel.
Investigation 2
Investigate art gallery problems for those polygons which arise as the boundaries of polyominoes.
What are examples of applications of polyominoes?
When one looks at the nets of a (regular) cube we find that there are 11 hexaminoes that fold to a 1x1x1 cube. This raises a variety of new lines of research about polyominoes which involve folding polyominoes to various "bricks." An axbxc brick is a solid which is combinatorially equivalent to a cube (as a graph) and which metrically has edges with the lengths a, b, and c (positive integers). Consider for example the polyomino below (Figure 6):
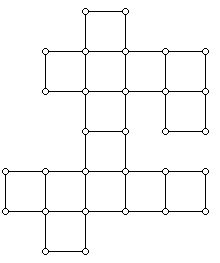
This polyomino has 14 squares and it turns out that it will fold to a 1x1x3 brick! This raises the question of whether there are always polyominoes that do not have holes that fold to 1x1xm bricks for every choice of m.
Investigation 3
Study those polyominoes that have no holes and which will fold to bricks, in particular to 1x1xm bricks.
An isometry is a (Euclidean) distance preserving transformation of the plane onto itself. Isometries include translations, reflections, rotations, and glide reflections. Some polyominoes have only the identity as a symmetry but many of them have relatively large symmetry groups. For example, the polyomino in Figure 3 has rotational symmetries and mirror (reflection) symmetries.
7. What is the symmetry group of the polyomino in Figure 3? Does this polyomino have the same or a different symmetric group from the symmetry group of the square (which can be thought of as a polyomino)? If we consider this polyomino as a graph (rather than as a metrical object) what is the symmetry group of the graph involved?
A mapping of a graph onto itself (that is, a mapping of the vertex set onto the vertex set so that edges are preserved) is called the automorphism of the graph. The collection of all automorphism of a graph (there is always at least one, the identity mapping) is called the automorphism group of the graph.
8. Is the automorphism group of the graph in Figure 3 isomorphic to the automorphism group of the metrical polyomino that is shown there?
Applications
In addition to the guard problem above, polyominoes have been used as a model of cell growth problems which have been applied to modeling the growth and control of fires, cancer cells, and epidemics. Problems about nets have applications to packaging design questions. A company designing cereal boxes may want an efficient layout of the nets of bricks within a rectangle.
As you can see polyominoes offer teachers and students a wide variety of "playgrounds" in which to formulate and solve geometrical problems. The proof techniques involved are ones that are valuable in a wide variety of geometrical and other situations: parity arguments and mathematical induction, etc.
References
There are two "classical books" devoted to polyominoes.
Golomb, S., Polyominoes: Puzzles, Patterns, Problems, and Packings, rev. enl. 2nd ed., Princeton University Press, Princeton 1995.
Martin, G., Polyominoes: Puzzles and Problems in Tiling, MAA, Washington, 1991.
Many of Martin Gardner's books contain chapters which are devoted to the many aspects of polyominoes.
There are lots of materials available on the web devoted to polyominoes.
For folding and unfolding problems and a broad survey of discrete geometry:
E. Demaine and J. O'Rourke, Geometric Folding Algorithms, Cambridge U. Press, New York, 2007
J. Goodman and J. O'Rourke, Handbook of Discrete and Computational Geometry, Chapman & Hall/CRC, Boca Raton, 2004.